728x90
반응형
1. DFS (Depth-First Search)
- DFS는 깊이 우선 탐색이라고도 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
- DFS는 스택 자료구조(혹은 재귀 함수)를 이용하며, 구체적인 동작 과정은 다음과 같다.
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
- 동작 예시
- [Step 0] 그래프를 준비한다. (방문 기준: 번호가 낮은 인접 노드부터)
- 시작 노드: 1

- 시작 노드: 1
- [Step 1] 시작 노드인 ‘1’을 스택에 삽입하고 방문 처리한다.

- [Step 2] 스택의 최상단 노드인 ‘1’에 방문하지 않은 인접 노드 ‘2’, ‘3’, ‘8’이 있다.
- 이 중에서 가장 작은 노드인 ‘2’를 스택에 넣고 방문 처리한다.
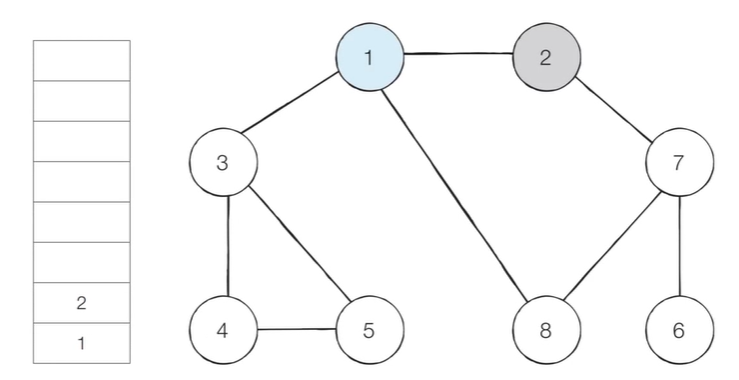
- 이 중에서 가장 작은 노드인 ‘2’를 스택에 넣고 방문 처리한다.
- [Step 3] 스택의 최상단 노드인 ‘2’에 방문하지 않은 인접 노드 ‘7’이 있다.
- 따라서 ‘7’번 노드를 스택에 넣고 방문 처리한다.
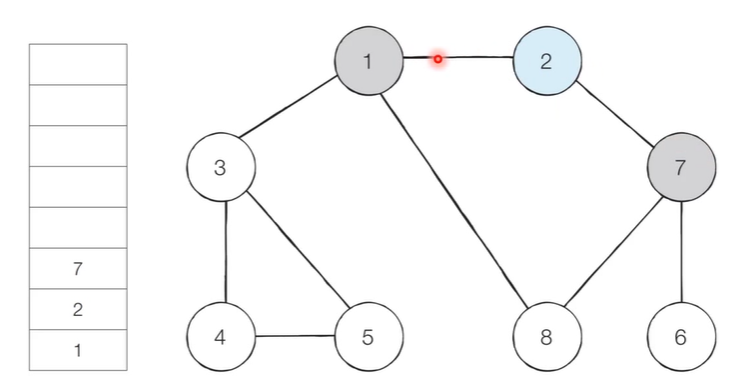
- 따라서 ‘7’번 노드를 스택에 넣고 방문 처리한다.
- [Step 4] 스택의 최상단 노드인 ‘7’에 방문하지 않은 인접 노드 ‘6’, ‘8’이 있다.
- 이 중에서 가장 작은 노드인 ‘6’을 스택에 넣고 방문 처리한다.

- 이 중에서 가장 작은 노드인 ‘6’을 스택에 넣고 방문 처리한다.
- [Step 5] 스택의 최상단 노드인 ‘6’에 방문하지 않은 인접 노드가 없다.
- 따라서 스택에서 ‘6’번 노드를 꺼낸다.
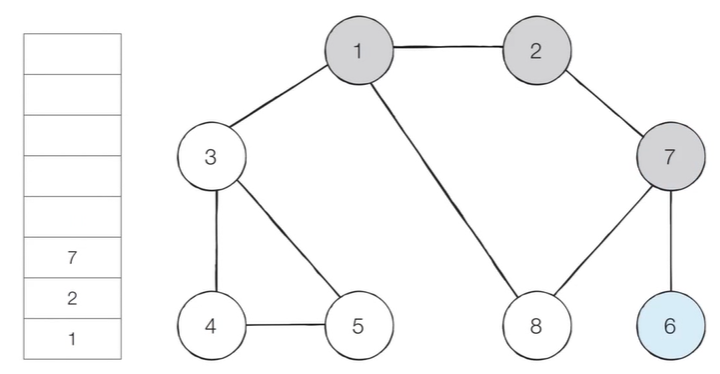
- 따라서 스택에서 ‘6’번 노드를 꺼낸다.
- [Step 6] 스택의 최상단 노드인 ‘7’에 방문하지 않은 인접 노드가 ‘8’이 있다.
- 따라서 ‘8’번 노드를 스택에 넣고 방문 처리한다.
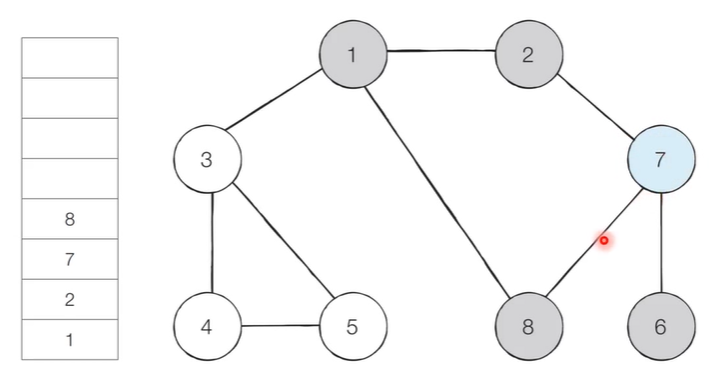
- 따라서 ‘8’번 노드를 스택에 넣고 방문 처리한다.
- 이러한 과정을 반복하였을 때 전체 노드의 탐색 순서(스택에 들어간 순서)는 다음과 같다.
- 탐색 순서: 1 → 2 → 7 → 6 → 8 → 3 → 4 → 5

- 탐색 순서: 1 → 2 → 7 → 6 → 8 → 3 → 4 → 5
- [Step 0] 그래프를 준비한다. (방문 기준: 번호가 낮은 인접 노드부터)
- 소스 코드 (Python)
- 보통 노드의 번호가 1번부터 시작인 경우가 많으므로 인덱스 0의 데이터는 비워둔다. 따라서 배열 크기를 원래 데이터 개수보다 한개 더 많게 잡는다.
- ex) 1번 노드와 연결되어 있는 노드는 2, 3, 8
# DFS 메서드 정의 def dfs(graph, v, visited): # 현재 노드를 방문 처리 visited[v] = True print(v, end=" ") # 현재 노드와 연결된 다른 노드를 재귀적으로 방문 for i in graph[v]: if not visited[i]: dfs(graph, i, visited) # 각 노드가 연결된 정보를 표현 (2차원 리스트) graph = [ [], [2, 3, 8], [1, 7], [1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8], [1, 7] ] # 각 노드가 방문된 정보를 표현 (1차원 리스트) visited = [False] * 9 # 정의된 DFS 함수 호출 dfs(graph, 1, visited) # 1 2 7 6 8 3 4 5
- 소스 코드 (Java)
import java.util.*; public class Main { public static boolean[] visited = new boolean[9]; public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>(); // DFS 함수 정의 public static void dfs(int x) { // 현재 노드를 방문 처리 visited[x] = true; System.out.print(x + " "); // 현재 노드와 연결된 다른 노드를 재귀적으로 방문 for (int i = 0; i < graph.get(x).size(); i++ { int y = graph.get(x).get(i); if(!visited[y]) dfs(y); } } public static void main(String[] args) { // 그래프 연결된 내용 생략 // dfs(1) } }
2. BFS (Breadth-First Search)
- BFS는 너비 우선 탐색이라고도 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘
- BFS는 큐 자료구조를 이용하며, 구체적인 동작 과정은 다음과 같다.
- 탐색 시작 노드를 큐에 삽입하고 방문 처리한다.
- 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
- 동작 예시
- [Step 0] 그래프를 준비한다. (방문 기준: 번호가 낮은 인접 노드부터)
- 시작 노드: 1

- 시작 노드: 1
- [Step 1] 시작 노드인 ‘1’을 큐에 삽입하고 방문 처리한다.

- [Step 2] 큐에서 노드 ‘1’을 꺼내 방문하지 않은 인접 노드 ‘2’, ‘3’, ‘8’을 큐에 삽입하고 방문 처리한다.

- [Step 3] 큐에서 노드 ‘2’를 꺼내 방문하지 않은 인접 노드 ‘7’을 큐에 삽입하고 방문 처리한다.

- [Step 4] 큐에서 노드 ‘3’를 꺼내 방문하지 않은 인접 노드 ‘4’, ‘5를 큐에 삽입하고 방문 처리한다.

- [Step 5] 큐에서 노드 ‘8’를 꺼내고 방문하지 않은 인접 노드가 없으므로 무시한다.

- 이러한 과정을 반복하여 전체 노드의 탐색 순서(큐에 들어간 순서)는 다음과 같다.
- 탐색 순서: 1 → 2 → 3 → 8 → 7 → 4 → 5 → 6

- 탐색 순서: 1 → 2 → 3 → 8 → 7 → 4 → 5 → 6
- [Step 0] 그래프를 준비한다. (방문 기준: 번호가 낮은 인접 노드부터)
- 소스 코드 (Python)
from collections import deque # BFS 메서드 정의 def bfs(graph, start, visited): # 큐(Queue) 구현을 위해 deque 라이브러리 사용 queue = deque([start]) # 현재 노드를 방문 처리 visited[start] = True # 큐가 빌 때까지 반복 while queue: # 큐에서 하나의 원소를 뽑아 출력 v = queue.popleft() print(v, end=" ") # 아직 방문하지 않은 인접한 원소들을 큐에 삽입 for i in graph[v]: if not visited[i]: queue.append(i) visited[i] = True # 각 노드가 연결된 정보를 표현 (2차원 리스트) graph = [ [], [2, 3, 8], [1, 7], [1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8], [1, 7] ] # 각 노드가 방문된 정보를 표현 (1차원 리스트) visited = [False] * 9 # 정의된 DFS 함수 호출 bfs(graph, 1, visited) # 1 2 3 8 7 4 5 6 - 소스 코드 (Java)
import java.util.*; public class Main { public static boolean[] visited = new boolean[9]; public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>(); // BFS 함수 정의 public static void bfs(int start) { Queue<Integer> q = new LinkedList<>(); q.offer(start); // 현재 노드를 방문 처리 visited[x] = true; while(!q.isEmpty()) { // 큐에서 하나의 원소를 뽑아 출력 int x = q.poll(); System.out.print(x + " "); // 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입 for(int i = 0; i < graph.get(x).size(); i++) { int y = graph.get(x).get(i); if(!visted[y]) { q.offer(y); visited[y] = true; } } } } // main 함수 생략 }
728x90
반응형
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 플로이드 워셜 알고리즘 (0) | 2024.02.03 |
|---|---|
| [자료구조] 다익스트라 알고리즘 (0) | 2024.02.03 |
| [자료구조] 정렬 알고리즘 비교 (0) | 2024.02.01 |
| [자료구조] 퀵 정렬과 계수 정렬 (0) | 2024.02.01 |
| [자료구조] 선택 정렬과 삽입 정렬 (0) | 2024.01.30 |