728x90
반응형
모든 출발지에서 다른 모든 출발지까지 최단 경로 계산
1. 플로이드 워셜(Floyd-Warshall) 알고리즘
- 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다.
- 플로이드 워셜(Floyd-Warshall) 알고리즘은 다익스트라 알고리즘과 마찬가지로 단계별로 거쳐 가는 노드를 기준으로 알고리즘을 수행한다.
- 다만 매 단계마다 방문하지 않은 노드 중에 최단 거리를 갖는 노드를 찾는 과정이 필요하지 않다.
- 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장한다.
- 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속한다.
- 점화식에 맞게 3중 반복문을 이용하여 2차원 테이블을 갱신한다.
- 다익스트라 알고리즘과 비교했을 때 구현 난이도는 쉬운 편인데 시간 복잡도는 O(N^3)이다.
- 노드의 개수가 적은 상황에서 효과적으로 사용할 수 있으며 노드나 간선의 개수가 많으면 다익스트라 알고리즘을 사용해야 한다.
- 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인한다.
- a부터 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사한다.
- 점화식

- 동작 과정
- [초기 상태] 그래프를 준비하고 최단 거리 테이블을 초기화한다.

- [Step 1] 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
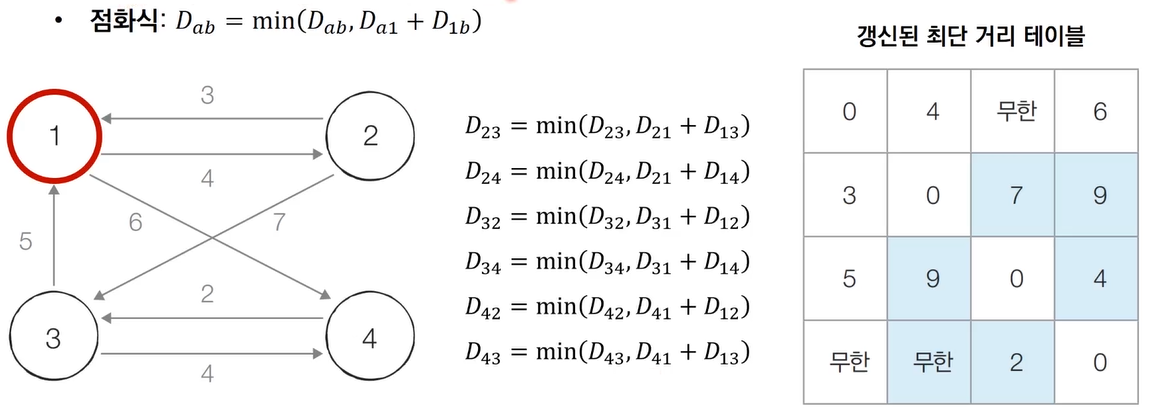
- [Step 2] 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

- [Step 3] 3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

- [Step 4] 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

- [초기 상태] 그래프를 준비하고 최단 거리 테이블을 초기화한다.
- 소스코드 (Python)
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정 # 노드의 개수 및 간선의 개수를 입력받기 n = int(input()) m = int(input()) # 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화 graph = [[INF] * (n + 1) for _ in range(n + 1)] # 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화 for a in range(1, n + 1): for b in range(1, n + 1): if a == b: graph[a][b] = 0 # 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화 for _ in range(m): # A에서 B로 가는 비용은 C라고 설정 a, b, c = map(int, input().split()) graph[a][b] = c # 점화식에 따라 플로이드 워셜 알고리즘을 수행 for k in range(1, n + 1): for a in range(1, n + 1): for b in range(1, n + 1): graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]) # 수행된 결과를 출력 for a in range(1, n + 1): for b in range(1, n + 1): # 도달할 수 없는 경우, 무한(INFINITY)이라고 출력 if graph[a][b] == 1e9: print("INFINITY", end=" ") # 도달할 수 있는 경우 거리를 출력 else: print(graph[a][b], end=" ") print() - 소스코드 (Java)
import java.util.*; public class Main { public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정 // 노드의 개수(N), 간선의 개수(M) // 노드의 개수는 최대 500개라고 가정 public static int n, m; // 2차원 배열(그래프 표현)를 만들기 public static int[][] graph = new int[501][501]; public static void main(String[] args) { Scanner sc = new Scanner(System.in); n = sc.nextInt(); m = sc.nextInt(); // 최단 거리 테이블을 모두 무한으로 초기화 for (int i = 0; i < 501; i++) { Arrays.fill(graph[i], INF); } // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화 for (int a = 1; a <= n; a++) { for (int b = 1; b <= n; b++) { if (a == b) graph[a][b] = 0; } } // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화 for (int i = 0; i < m; i++) { // A에서 B로 가는 비용은 C라고 설정 int a = sc.nextInt(); int b = sc.nextInt(); int c = sc.nextInt(); graph[a][b] = c; } // 점화식에 따라 플로이드 워셜 알고리즘을 수행 for (int k = 1; k <= n; k++) { for (int a = 1; a <= n; a++) { for (int b = 1; b <= n; b++) { graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]); } } } // 수행된 결과를 출력 for (int a = 1; a <= n; a++) { for (int b = 1; b <= n; b++) { // 도달할 수 없는 경우, 무한(INFINITY)이라고 출력 if (graph[a][b] == INF) { System.out.print("INFINITY "); } // 도달할 수 있는 경우 거리를 출력 else { System.out.print(graph[a][b] + " "); } } System.out.println(); } } } - 성능 분석
- 노드의 개수가 N개일 때 알고리즘 상으로 N번의 단계를 수행한다.
- 각 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려한다.
- 따라서 플로이드 워셜 알고리즘의 총 시간 복잡도는 O(N^3)이다.
- 노드의 개수가 N개일 때 알고리즘 상으로 N번의 단계를 수행한다.
728x90
반응형
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 서로소 집합을 판단하기 위한 Union Find 자료구조 (0) | 2024.02.04 |
|---|---|
| [자료구조] 벨만 포드 알고리즘 (0) | 2024.02.03 |
| [자료구조] 다익스트라 알고리즘 (0) | 2024.02.03 |
| [자료구조] DFS와 BFS (0) | 2024.02.02 |
| [자료구조] 정렬 알고리즘 비교 (0) | 2024.02.01 |